Khám phá và sáng tạo hình học phẳng – 25/02/25
Bài toán 1. Cho tam giác ABC nội tiếp (O), có đường cao AH, L là điểm Lemoine. M, N lần lượt là trung điểm BC, AH. Chứng minh rằng M, N, L thẳng hàng.
Hướng dẫn và phân tích.
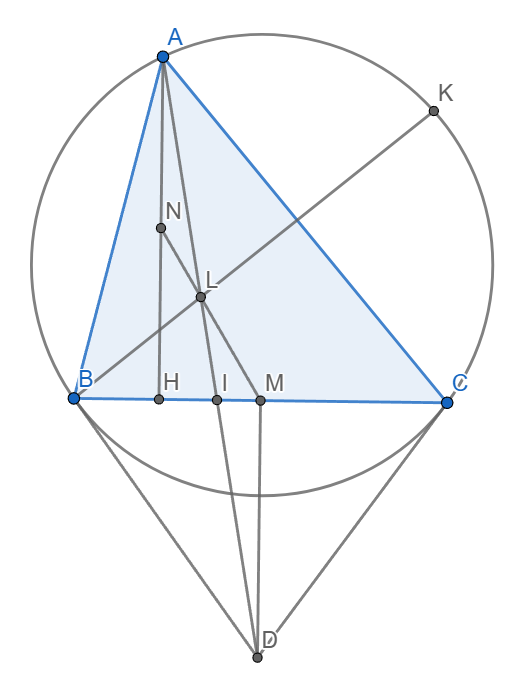
Tiếp tuyến qua B và C của (O) cắt nhau tại D.
AL cắt BC tại I, BL cắt lại (O) tại K. Ta có ABCK là tứ giác điều hoà.
M(DLAH) = (DLAI) = B(DLAI) = (BKAC) = -1. (1)
Lại có MD là trung trực BC nên MD // AH, suy ra M(DNAH) = -1. (2)
Từ (1) và (2) suy ra đpcm.
Bài toán 2. Cho tam giác ABC nội tiếp (O). Tiếp tuyến qua A và B của (O) cắt nhau tại P, tiếp tuyến qua B và C của (O) cắt nhau tại Q. K, M, N lần lượt là trung điểm BC, CA, AB. H là hình chiếu của A trên MN. HP cắt KM tại X, HQ cắt KN tại Y. Chứng minh rằng MN, PQ, XY đôi một song song hoặc đồng quy.
Hướng dẫn và phân tích.
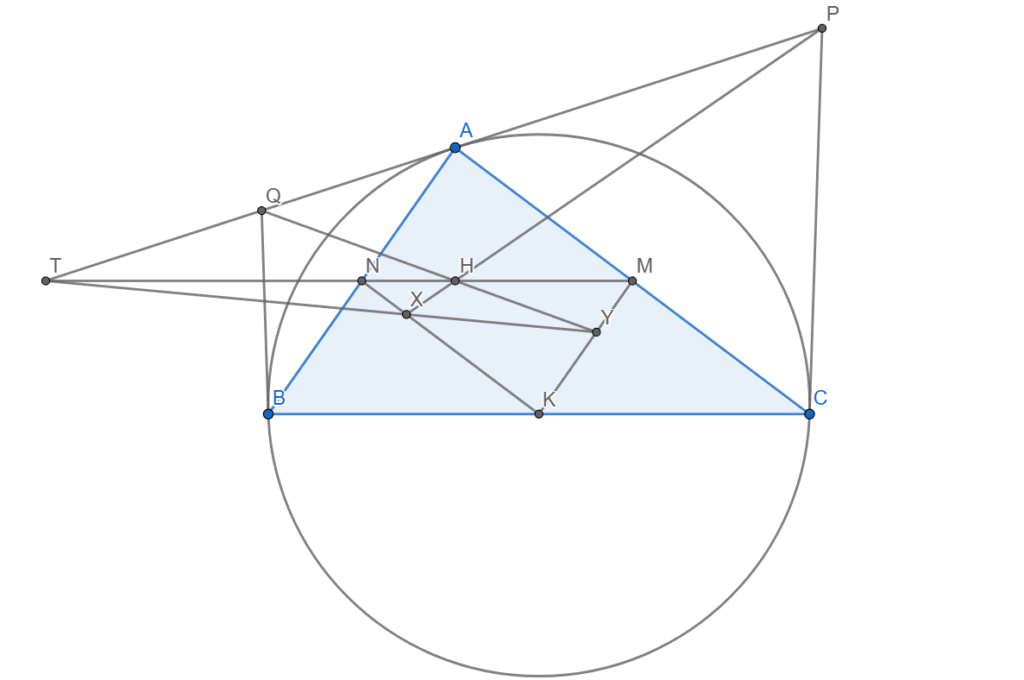
Trường hợp tam giác ABC cân tại A dễ dàng chứng minh 3 đường thẳng đôi một song song.
Xét trường hợp AB < AC:
Với cách định nghĩa các điểm X và Y, ta nghĩ đến ngay định lý Desargues. Áp dụng định lý Desargues cho tam giác HPQ và KMN, khi đó ta cần chứng minh HK, PM, QN đồng quy. (1)
Gọi L là điểm Lemoine của tam giác ABC. Sử dụng kết quả bài toán 2, thu được H, K, L thẳng hàng; (1) tương đương với LK, PM, QN đồng quy.
Đến đây áp dụng định lý Desargues một lần nữa, phần còn lại của bài toán tương đương với bài toán sau:
Bài toán 3. Cho tam giác ABC nội tiếp (O). Tiếp tuyến qua A và B của (O) cắt nhau tại P, tiếp tuyến qua B và C của (O) cắt nhau tại Q. K, M, N lần lượt là trung điểm BC, CA, AB. BQ cắt CP tại L. LP cắt KM tại X, LQ cắt KN tại Y. Chứng minh rằng MN, PQ, XY đôi một song song hoặc đồng quy.
Hướng dẫn và phân tích.
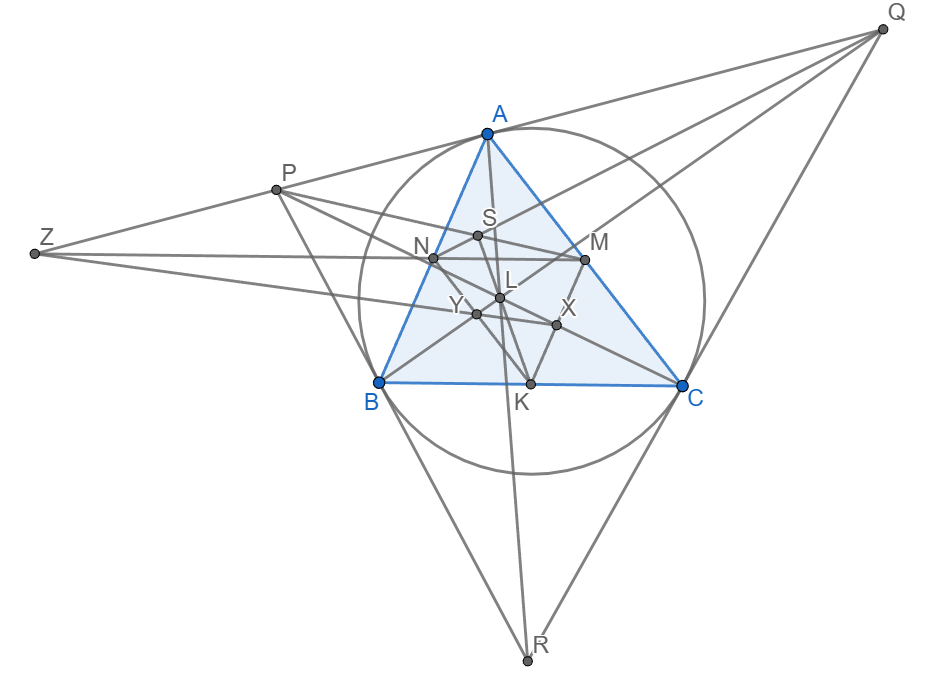
AB = AC => ez (3 đường thẳng đôi một song song). Xét AB < AC:
Gọi Z là giao điểm MN và PQ.
Do AZ là tiếp tuyến của (ABC) và MN // BC nên AZ cũng là tiếp tuyến của (AMN). Ta có:
ZM/ZN = ZM/ZA.ZA/ZN = sin ZAM/sin AMZ × sin ANZ/sin ZAN = sin ANM/sin AMN × sin ANM/sin AMN = (AM/AN)2
CX là đường đối trung của tam giác CAB nên cũng là đối trung của tam giác CMK, do đó: XK/XM = (CK/CM)2. Tương tự: YN/YK = (BN/BK)2.
=> YN/YK × XK/XM × ZM/ZN = (BN/BK × CK/CN × AN/AM)2 = 1
Theo định lý Menelaus đảo ta có X, Y, Z thẳng hàng, bài toán được giải quyết.
Bằng cách đổi mô hình, ta thu được bài toán sau:
Bài toán 4. Cho tam giác ABC ngoại tiếp (I), có G là điểm Gergone. (I) tiếp xúc BC, CA, AB theo thứ tự tại D, E, F. N, K, L lần lượt là trung điểm EF, DE, DF. H là hình chiếu của D trên KL. BK cắt CL tại S. Chứng minh rằng 4 điểm S, H, G, N thẳng hàng.
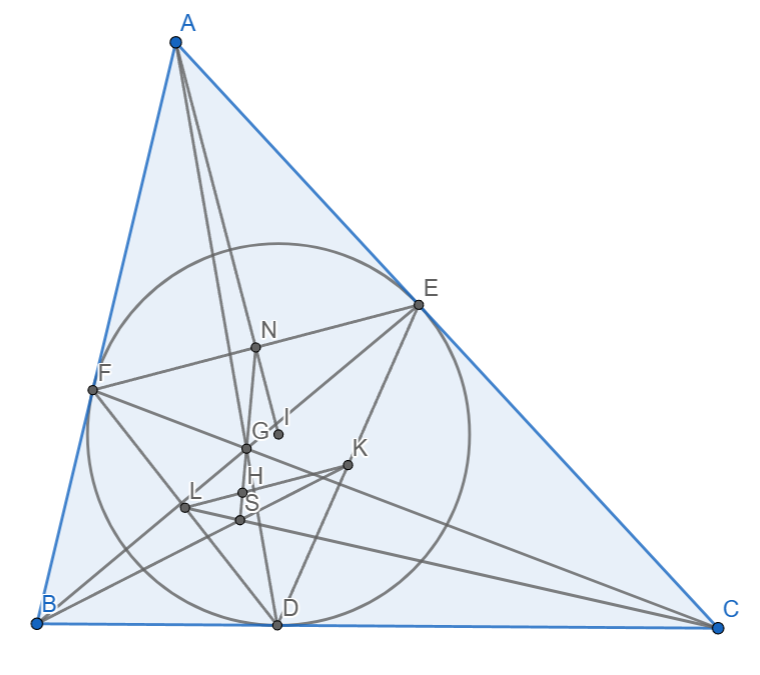
Tiếp theo, ta có bài toán sau đây:
Bài toán 5. Cho tam giác ABC và một điểm K bất kì nằm trong tam giác. KA, KB, KC theo thứ tự cắt BC, CA, AB tại D, E, F. M, N, P, Q lần lượt là trung điểm BC, DK, DE, DF. Chứng minh rằng BP, CQ, MN đồng quy.
Hướng dẫn và phân tích.
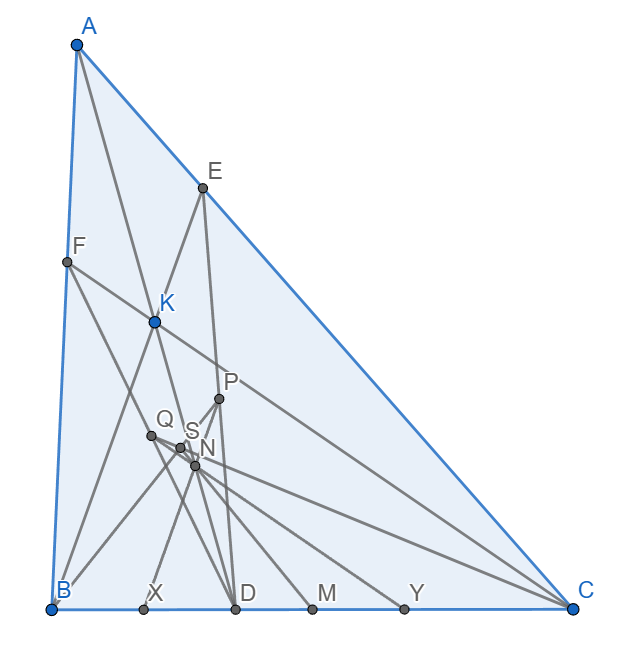
Gọi X, Y lần lượt là trung điểm DB, DC.
Phép vị tự tâm D tỉ số 2 biến X, N, P theo thứ tự thành B, K, E. Do đó P, N, X thẳng hàng và PX/PN = EB/EK.
Tương tự: Q, N, Y thẳng hàng và QY/QN = FC/FK.
BP cắt CQ tại S, SN cắt BC tại M’.
Áp dụng định lý Menelaus:
BX/BM’ = PX/PN × SN/SM (tam giác XNM’; B, S, P thẳng hàng)
CY/CM’ = QY/QN × SN/SM’ (tam giác YNM’; C, S, Q thẳng hàng)
=> BX/BM’ : CY/CM’ = PX/PN : QY/QN = EB/EK × FK/FC. (2)
Áp dụng định lý Ceva cho tam giác KBC có KD, BF, CE đồng quy tại A:
EB/EK × FK/FC = DB/DC = BX/CY. (2)
Từ (1) và (2) suy ra BM’ = CM’, hay M’ là trung điểm BC. Do đó M’ trùng M, ta có đpcm.
Kết hợp bài toán 4 và 5, ta thu được bài toán sau:
Bài toán 6. Cho tam giác ABC ngoại tiếp (I). (I) tiếp xúc BC, CA, AB theo thứ tự tại D, E, F. M, N, K, L lần lượt là trung điểm BC, DG, DE, DF. H là hình chiếu của D trên KL. Chứng minh rằng 4 đường thẳng GH, MN, BK, CL đồng quy.
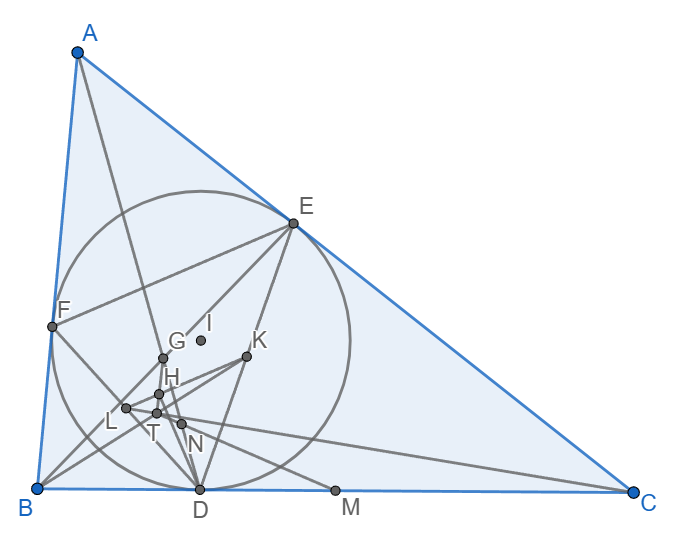
Cuối cùng, ta có bài toán:
Bài toán 7. Cho tam giác ABC nội tiếp (O), ngoại tiếp (I), có G là điểm Gergone. (BIC) cắt (I) tại 2 điểm A1, A2. Gọi ωA là đường tròn ngoại tiếp tam giác (AA_1A_2). ωB và ωC định nghĩa tương tự. Chứng minh rằng G là tâm đẳng phương của 3 đường tròn ωA, ωB, ωC.
Hướng dẫn và phân tích.
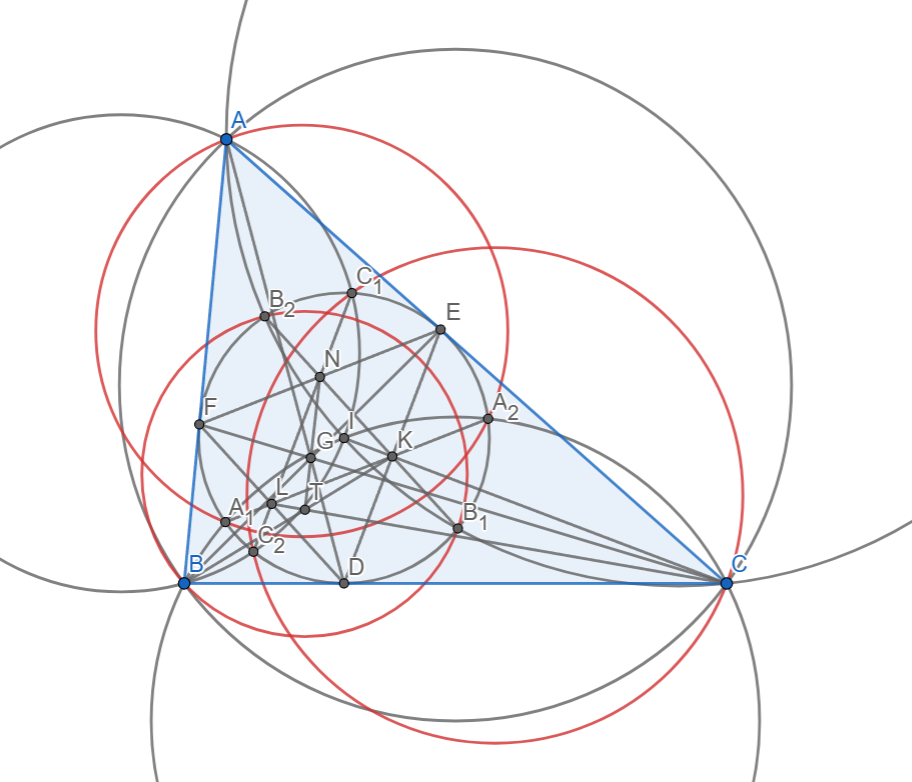
Định nghĩa các điểm D, E, F, N, K, L giống bài toán 6.
Ta chứng minh được: K, L, A1, A2 thẳng hàng. (Đây là một bài toán hay, nhiều cách giải nhưng không khó, xin dành cho bạn đọc)
K, N, B1, B2 thẳng hàng; N, L C1, C2 thẳng hàng.
Tiếp theo ta tìm trục đẳng phương của ωB và ωC, với ý tưởng là xét thêm 1 đường tròn (Z) nào đó và tìm tâm đẳng phương của (Z), ωB, ωC.
- Chọn (Z) = (I). Trục đẳng phương của (I) và ωB là B1B2, Trục đẳng phương của (I) và ωC là C1C2, B1B2 cắt C1C2 tại N nên N là tâm đẳng phương của 3 đường tròn. (1)
- Chọn (Z) = (BIC):
Do I, C, B1, B2 đồng viên nên KB1.KB2 = KI.KC => PK/ωB = PK/(IBC). Do đó BK là trục đẳng phương của ωB và (BIC).
Tương tự CL là trục đẳng phương của ωC và (BIC).
Gọi T là giao điểm BK và CL thì T là tâm đẳng phương của (BIC), ωB, ωC. (2)
Từ (1) và (2) suy ra NT là trục đẳng phương của ωB và ωC.
Áp dụng bài toán 6, ta có BK, CL, GN đồng quy, do đó G thuộc trục đẳng phương của ωB và ωC. Tương tự G cũng thuộc trục đẳng phương của ωB và ωA, ta có đpcm.
Mọi người có ý tưởng phát triển bài viết hoặc cách giải khác thì nhắn tin cho Tạp chí Tri Thức Trẻ: https://www.facebook.com/tapchittt, admin sẽ chỉnh sửa và cập nhật thêm cho bài viết. Xin chân thành cảm ơn!
Comments (0)