tttbooks

Cho tam giác ABC. Điểm D đối xứng A qua BC. Lấy các điểm E, F trên (DBC) sao cho AE, AF đẳng giác góc BAC. DE, DF cắt BC lần lượt tại K, L. Chứng minh rằng (AEF) tiếp xúc (AKL).

Lời giải.

Bổ đề: Cho tam giác ABC nội tiếp (O) có đường cao AH. Khi đó AH và AO đẳng giác góc BAC. (1)

Đây là kết quả quen thuộc, bạn đọc tự chứng minh.

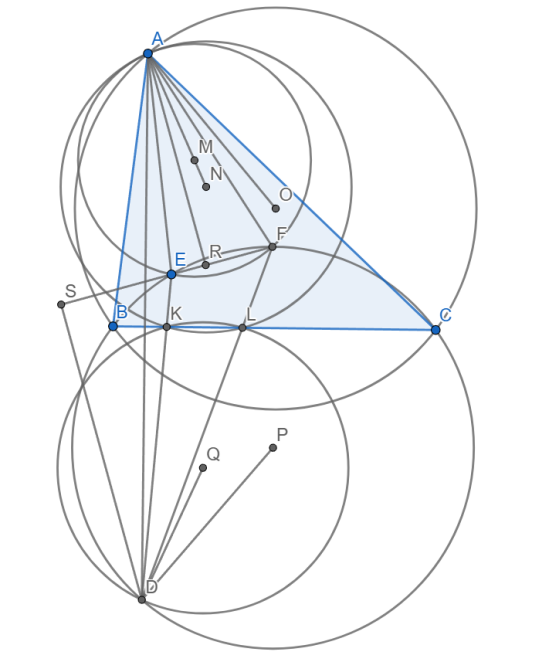
M, N, O, P, Q lần lượt là tâm (AEF), (AKL), (ABC), (DBC), (DKL).

R, S là hình chiếu của A, D trên EF.

Từ bổ đề (1) suy ra: DS, DP đẳng giác góc EDF; DA, DQ đẳng giác góc KDL

=> <SDA = <PDQ. (2)

Do SD // AR nên <SDA = <RAD. (3)

N, O đối xứng Q, P qua BC => <PDQ = <OAN. (4)

(2), (3), (4) => <RAD = <OAN. (5)

(1) => <DAB = <OAC => <DAE = <OAF. (6)

(5), (6) =><RAE = <NAF. Lại có <RAE = <MAF (bổ đề (1)) nên <NAF = <MAF

Do đó A, M, N thẳng hàng, dẫn đến (AEF) tiếp xúc (AKL) tại A. (đpcm)